Let us know the basic structure of syllogisms
A syllogism has three parts-
(a) Major premise (b) Minor premise (c) Conclusion
The major term in the major premise, which forms the predicate of the conclusion, and the minor term in the minor premise, which forms the subject of the conclusion. The categorical term in common in the premises is called the "middle term".
For example:
Major premise: All birds are animals.
Minor premise: All peacocks are birds.
Conclusion: All peacocks are animals.
In this example, "animal" is the major term and predicate of the conclusion, " peacock " is the minor term and subject of the conclusion, and "bird" is the middle term.
Think of each term as representing a category
I. Universal Affirmative: All (100%)
II. Universal Negative: No (100%)
III. Particular Affirmative: Some (50%)
IV. Particular Negative: Some not (50%)
Understand each prefix as expressed as "Some/all/no A is/are [not] B," with four possible variation.
· The universal affirmative (symbolized as A) is expressed as
"all A is/are B," abbreviated as AAB.
Example:
Statement: All birds are animals
All peacocks are birds
Conclusion: All peacocks are animals
- The universal negative (symbolized as E) is expressed as
- "no A is/are B," abbreviated as AEB.
- The particular affirmative (symbolized as I) is expressed as
- "some A is/are B," abbreviated as AIB.
- The particular negative (symbolized as O) is expressed as
- "some A is/are not B," abbreviated as AOB.
Determine the venn-diagram of the syllogism.
Depending on whether the middle term serves as subject or predicate in the premises, a syllogism may be classified as
one of four possible figures:
First figure: The middle term serves as subject in the major premise and predicate in the minor premise. Thus, first figure takes the form:
Major premise: M-P..........e.g., "All birds are animals"
Minor premise: S-M..........e.g., "All parrots are birds"
Conclusion: S-P..........e.g., "All parrots are animals".
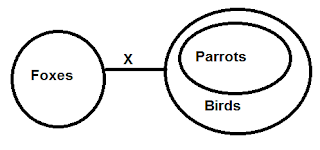
Second figure: The middle term serves as predicate in the major premise and predicate in the minor premise. Thus, second figure takes the form:
Major premise: P-M..........e.g., "No foxes are birds"
Minor premise: S-M..........e.g., "All parrots are birds"
Conclusion: S-P..........e.g., "No parrots are foxes".
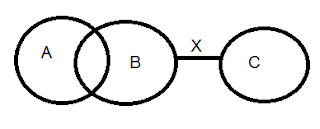
Third figure: The middle term serves as subject in the major premise and subject in the minor premise. Thus, third figure takes the form:
Major premise: M-P..........e.g., "All birds are animals"
Minor premise: M-S..........e.g., "All birds are mortals"
Conclusion: S-P..........e.g., "Some mortals are animals"
Fourth figure: The middle term serves as predicate in the major premise and subject in the minor premise. Thus, fourth figure takes the form:
Major premise: P-M..........e.g., "No birds are cows"
Minor premise: M-S..........e.g., "All cows are animals"
Conclusion: S-P..........e.g., "Some animals are not birds".
We are explaining the concept of Syllogism with some examples by using some simple rules.
First and foremost have a quick glance at the Main rules to solve Syllogism Problems…
All + All
1. Statements: All smarts are dumb.
All bad are smarts.
Total Definite Conclusions:
ALL
All bad are dumb.
SOME
Some bad are smarts.
Some bad are dumb.
SOME (REVERSE)
Some smarts are bad.
Some dumb are bad.
All + No
2. Statements: All cities are houses.
No lands is a cities.
Total Definite Conclusions:
NO
All cities are not lands.
Or
No cities is a lands.
SOME
Some cities are houses.
SOME (REVERSE)
Some houses are cities.
SOME NOT
Some cities are not lands.
Some houses are not lands.
SOME NOT (REVERSE)
Some lands are not cities.
All + Some
3. Statements: All kitchens are closets.
Some closets are shelves.
Total Definite Conclusions:
Some
Some kitchens are closets.
Some (Reverse)
Some closets are kitchens.
Some shelves are closets.
Some + All
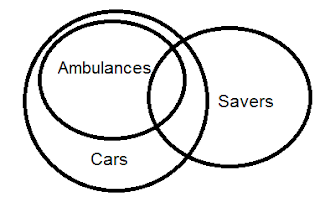
4. Statements: Some ambulances are savers.
All ambulances are cars.
Total Definite Conclusions:
SOME
Some ambulances are savers.
Some ambulances are cars.
Some cars are savers.
SOME (REVERSE)
Some savers are ambulances.
Some cars are ambulances.
Some savers are cars.
Some + No
5. Statements: Some A are B.
No B is a C.
Total definite conclusions:
ALL NOT / NO (REVERSE)
No C is a B.
SOME NOT
Some B are not C.
Some A are not C.
SOME NOT (REVERSE)
Some C are not B.
SOME (REVERSE)
Some B are A.
Some + Some
6. Statements: Some A are B.
Some B are C.
Total definite conclusions:
SOME (REVERSE)
Some B are A
Some C are B
No + All
7. Statements: No segment is a translator.
All translators are website.
Total Definite Conclusions:
NO/ALL NOT (REVERSE)
No translator is a segment.
SOME NOT
Some segments are not translator.
Some websites are not segment.
SOME NOT (REVERSE)
Some translators are not segment.
SOME
Some websites are translators.
SOME (REVERSE)
Some translators are website.
No + Some
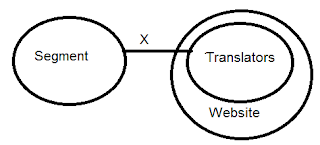
8. Statements: No segment is a translator.
Some translators are website.
Total Definite Conclusions:
NO/ALL NOT (REVERSE)
No translator is a segment.
SOME NOT
Some segments are not translator.
Some websites are not segment.
SOME NOT (REVERSE)
Some translators are not segment.
SOME (REVERSE)
Some websites are translator.
No + No
9. Statements: No dog is a brown.
No bull is a brown.
Total Definite Conclusions:
NO / ALL NOT (REVERSE)
No brown is a dogs.
No brown is a bulls.
SOME NOT
Some dogs are not brown.
Some brown are not bulls.
SOME NOT (REVERSE)
Some brown are not dogs.
Some bulls are not brown.
Lets discuss Either-Or condition in syllogism:
Complementary pair of conclusions:
Students are required to be more attentive in selecting complementary pair of conclusion, where neither of the conclusions is definitely true but a combination of both makes a complementary pair.
I. Complementary pair means Subject and Predicate are same in given statements.
II. One should be in positive and one should be in negative.
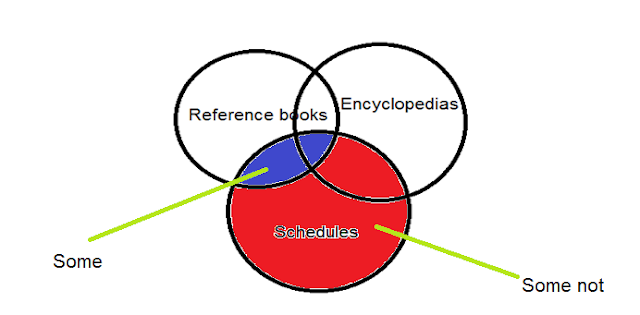
Example:
Statement: Some reference books are encyclopedias
Some encyclopedias are schedules
Conclusions:
I. Some reference books are schedules
II. Some schedules are not reference books
Explanation: Here,
I. Complimentary pair…….
II. + ve and – ve …….
Hence EITHER conclusion I OR conclusion II is true.
Special cases
Combinations Conclusion
A + E Either I or II follows
E + I Either I or II follows
I + O Either I or II follows
E + O Either I or II follows
IMPORTANT NOTE:
EITHER and OR case takes place between these three complimentary pairs only when they share same element between them and there have no relation between them.
Between ALL ……and SOME NOT………..
Between SOME……. and SOME NOT……….
Between SOME……… and NO……………
EITHER AND OR case should not take place when there is combination of ALL……….. and NO………………..