In SSC exam quantitative Aptitude section is more scoring and easy if you know the shorts tricks and formulas of all the topic. So, it is important to know the basic concept of all the topic so you can apply the short tricks and solve the question with the new concept in lesser time while giving the quiz. It will help you to score more marks from this section in less time period. Quantitative Aptitude section basically measures your mathematical and calculation approach of solving the question. SSC Quiz Of quantitative Aptitude section helps you to analysis your preparation level for upcoming SSC examination. Mahendra Guru provides you Quantitative Aptitude Quiz for SSC examination based on the latest pattern. So that you can practice on regular basis. It will definitely help you to score good marks in the exam. It is the most important section for all the govt exam like Insurance, SSC-MTS, SSC CPO , CGL, CHSL, State Level, and other Competitive exams.
You can clear your doubts before exam. Mahendra Guru also provides you an important note and study material for all subject and test through its website, Mahendra Guru App and YouTube channel apart from it Speed Test Portal. Most of these preparation products are also available for purchase on my shop. You can also visit Mahendras.org to get more information about our endeavour for your success. You can also study in details through our E-Mahendras Facebook and Mahendra Guru YouTube channel of Quantitative Aptitude.
Q.1-
If in a sale,
the discount given on a saree is equal to one-fourth of the marked price and
the loss due to this discount is 15%, then the ratio of the cost price to
the selling price is-
यदि किसी सेल में, साड़ी पर दी गई छूट अंकित मूल्य के एक - चौथाई मूल्य के बराबर है और इस छूट के कारण होने वाली हानि 15% है, तो लागत मूल्य और बिक्री मूल्य का अनुपात क्या होगा?
यदि किसी सेल में, साड़ी पर दी गई छूट अंकित मूल्य के एक - चौथाई मूल्य के बराबर है और इस छूट के कारण होने वाली हानि 15% है, तो लागत मूल्य और बिक्री मूल्य का अनुपात क्या होगा?
A. 15 :
17 B. 12 : 13 C. 3 : 4 D. 20 : 17
Q.2-
The side of a
square is 8 cm. If a square is made by joining the mid points of each sides of
this square and this process goes up to infinity. Calculate the sum of areas of
all the squares made.
एक वर्ग की भुजा 8 सेमी. है । वर्ग की प्रत्येक भुजा के मध्य बिन्दुओं को मिलाकर एक वर्ग बनाया जाता हैं और यह प्रक्रिया अनन्त तक चलती रहती है |। सभी बने हुये वर्ग के क्षेत्रफलों का योगफल की गणना कीजिए।
एक वर्ग की भुजा 8 सेमी. है । वर्ग की प्रत्येक भुजा के मध्य बिन्दुओं को मिलाकर एक वर्ग बनाया जाता हैं और यह प्रक्रिया अनन्त तक चलती रहती है |। सभी बने हुये वर्ग के क्षेत्रफलों का योगफल की गणना कीजिए।
A. 64 cm2 /सेमी. B. 32 cm2 /सेमी. C. 128 cm2 /सेमी. D. 256 cm2 /सेमी.
Q.3- AB is a chord to a circle and PAT is the tangent to the
circle at A. If ∠ BAT = 75o
and ∠ BAC = 45o, C being a point on the major arc
of circle, then ∠ ABC is equal
to-
AB एक वृत्त की जीवा है और PAT वृत्त के बिन्दु A पर स्पर्श रेखा है। यदि ∠ BAT = 75o और ∠ BAC = 45o तथा C वृत्त के दीर्घ चाप पर स्थित एक बिन्दु है, तो ∠ ABC है-
AB एक वृत्त की जीवा है और PAT वृत्त के बिन्दु A पर स्पर्श रेखा है। यदि ∠ BAT = 75o और ∠ BAC = 45o तथा C वृत्त के दीर्घ चाप पर स्थित एक बिन्दु है, तो ∠ ABC है-
A.
60o B. 50o C. 70o D. 90o
Q.4- A tree of height 'h' meters is broken by storm in such a
way that its top touches the ground at a distance of 'x' meters from the root.
Find the height at which the tree has broken. (Here h> x)
'h' मीटर ऊँचा एक वृक्ष आँधी के कारण इस प्रकार टूट जाता है कि उसका शीर्ष उसकी जड़ से 'x' मी. की दूरी पर जमीन को स्पर्श करता है। ज्ञात कीजिए कि वृक्ष कितनी ऊँचाई से टूटा है। (यहाँ h > x)
'h' मीटर ऊँचा एक वृक्ष आँधी के कारण इस प्रकार टूट जाता है कि उसका शीर्ष उसकी जड़ से 'x' मी. की दूरी पर जमीन को स्पर्श करता है। ज्ञात कीजिए कि वृक्ष कितनी ऊँचाई से टूटा है। (यहाँ h > x)
A. 
m/मी. B. 
m/मी.
m/मी. B. m/मी.C.
m/मी. D. 
m/मी.
Q.5-
A man borrows
some money at 3% simple interest per annum and lends it to somebody at 5%
interest to be compounded annually. By this he makes a profit of Rs.541 at the
end of 3 years. The money he borrowed was-
एक आदमी ने 3% साधारण वार्षिक ब्याज पर कुछ राशि उधार ली और उसे 5% वार्षिक चक्रवृद्धि ब्याज पर किसी को ऋण पर दे दिया। इस प्रकार उसने 3 वर्ष के अंत में रू. 541 लाभ कमाया। उसके द्वारा उधार ली गयी राशि थी-
एक आदमी ने 3% साधारण वार्षिक ब्याज पर कुछ राशि उधार ली और उसे 5% वार्षिक चक्रवृद्धि ब्याज पर किसी को ऋण पर दे दिया। इस प्रकार उसने 3 वर्ष के अंत में रू. 541 लाभ कमाया। उसके द्वारा उधार ली गयी राशि थी-
A. Rs.
8000 B. Rs. 12000 C. Rs. 15800 D. Rs. 18400
Q.6- A copper wire
is bent in the form of an equilateral triangle and has area
. If the same wire is bent into the form
of a circle, the area (in cm2) enclosed by the wire is (Take pi= 22 /7)
एक ताँबे के तार को मोड़कर एक समबाहु त्रिभुज बनाया गया है, जिसका क्षेत्रफल सेमी2
है। यदि उसी तार को मोड़कर एक वृत्त बना दिया जाए, तो उस वृत्त का क्षेत्रफल (pi= 22/7 मानकर) कितने
सेमी2 होगा?
सेमी2
है। यदि उसी तार को मोड़कर एक वृत्त बना दिया जाए, तो उस वृत्त का क्षेत्रफल (pi= 22/7 मानकर) कितने
सेमी2 होगा?
A. 388.5
cm2/सेमी.2 B.
346.5cm2/सेमी.2 C.
322.5 cm2/सेमी.2 D.286.5 cm2/सेमी.2
Q.7-
Base of the
right prism is an equilateral triangle. If its height reduced to one -fourth
and each side of the base is tripled , then the ratio of the volumes of the old
prism to the new prism is-
एक समलम्ब प्रिज्म का आधार एक समबाहु त्रिभुज है। यदि इसकी ऊॅचाई घटाकर एक चौथाई और आधार की प्रत्येक भुजा तीन गुना कर दी जाए तो पुराने प्रिज्म और नए प्रिज्म के आयतन का अनुपात ज्ञात कजिए।
एक समलम्ब प्रिज्म का आधार एक समबाहु त्रिभुज है। यदि इसकी ऊॅचाई घटाकर एक चौथाई और आधार की प्रत्येक भुजा तीन गुना कर दी जाए तो पुराने प्रिज्म और नए प्रिज्म के आयतन का अनुपात ज्ञात कजिए।
A. 7 : 9 B. 5 : 7 C. 4 : 9 D. 9 : 4
Q.8- In ΔABC, ∠A = ∠B = 600, AC = 
cm.
cm.
The lines AD
and BD intersect at D with ∠D = 900. If DB=
2 cm, then the length of AD is
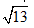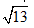ΔABC में, ∠A = ∠B = 600, AC = सेमी । AD और BD रेखाएँ एक दूसरे को बिन्दु D पर काटती हैं जहाँ∠D = 900 है। यदि DB
= 2 सेमी, तो AD की लम्बाई
कितनी होगी?
सेमी । AD और BD रेखाएँ एक दूसरे को बिन्दु D पर काटती हैं जहाँ∠D = 900 है। यदि DB
= 2 सेमी, तो AD की लम्बाई
कितनी होगी?
A. 8 cm/सेमी. B. 5 cm/सेमी. C. 4 cm/सेमी. D. 3 cm/सेमी.
Q.9- A rectangular sheet of metal is 40 cm by 15 cm. Equal
squares of side 4 cm. are cut off at the corners and
the remainder is folded up
to form an open rectangular box. The volume of the box is-
एक धातु की आयताकार चादर 40 सेमी ×15 सेमी की है। चारों कोनों से 4 सेमी भुजा के समान वर्ग काटे गए हैं। शेष चादर को मोड़कर एक खुला आयताकार सन्दूक बनाया गया है। सन्दूक का आयतन है-
एक धातु की आयताकार चादर 40 सेमी ×15 सेमी की है। चारों कोनों से 4 सेमी भुजा के समान वर्ग काटे गए हैं। शेष चादर को मोड़कर एक खुला आयताकार सन्दूक बनाया गया है। सन्दूक का आयतन है-
A.896
cm3/सेमी.2 B. 1288 cm3/सेमी.2 C. 985 cm3/सेमी.2 D.869 cm3/सेमी.2
Q.10-
The least value
of n, such that (1 + 3 + 32 + ... + 3n) exceeds 2000, is-
n का वह सबसे कम मान बताइए, जिससे (1 + 3 + 32 + ... + 3n) का मान 2000 से अधिक हो।
n का वह सबसे कम मान बताइए, जिससे (1 + 3 + 32 + ... + 3n) का मान 2000 से अधिक हो।
A. 3 B. 5 C. 7 D. 8
ANSWERS
Q.1- (D)
Q.2- (C)
Q.3- (A)
Q.4- (B)
Q.5- (A)Let the money borrowed by x Rs./ माना उधार ली गयी राशि गयी
धनराशि रू.x है
Q.6- (B)
Q.7- (C)
Q.8- (D)
Length of AD /AD की लम्बाई ==3cm./सेमी.
Q.9- (A)The volume of the box/ सन्दूक का आयतन
= 32 × 7 × 4
= 896 cm3/सेमी3
= 896 cm3/सेमी3
Q.10- (D)
a = 1, r = 34000 = 3n - 1
3n = 4001
According to question/प्रश्नानुसार
n = 8
