SSC CGL | CPO | CHSL Quiz : Quantitative Aptitude | 02-02-2022

Dear Readers,

As SSC  CGL | CPO |  CHSL  notification is out and candidates have started their preparation for this exam. Mahendras also has started special quizzes for this examination. This series of quizzes are based on the latest pattern of the SSC  CGL | CPO |  CHSL examination. Regular practice of the questions included in the quizzes will boost up your preparations and it will be very helpful in scoring good marks in the examination.

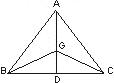
(1) 'G' is centroid of ΔABC if AG = BC then find ∠BGC.

'G' Δ ABC का केन्द्रक है यदि AG = BC तो ∠BGC ज्ञात कीजिये।

(A) 90o

(B) 30o

(C) 60o

(D) 120o

(2) A seller uses 920 gm in place of one kg to sell his goods. When he sells his articles at 15% gain on cost price, the actual percentage of profit is :

एक दुकानदार एक वस्तु को बेचते समय 1 किलो के स्थान पर 920 ग्राम का प्रयोग करता है यदि वह उसे वस्तु को बेचने पर पहले 15 % का लाभ होता है क्रय मूल्य पर तो अब उसका वास्तविक प्रतिशत क्या है ?

(A) 25

(B) 20

(C) 32

(D) 30

(3) The angle of elevation of the top of a tower from a point A on the ground is 30^o. On moving a distance of 20 m towards the foot of the tower to a point B, the angle of elevation increase to 60^o.The height of the tower is-

समतल पर स्थित किसी बिंदु A से टावर के शीर्ष का उन्नयन कोण 30^o हैं | टावर के पाद की ओर 20 मी . चलने पर उन्नयन कोण 60^o हो जाता हैं | टावर की उचाई ज्ञात कीजिये ।

(A) 10√3

(B) 20√3

(C) 5√3

(D) 15

(4) If x,y,z are non-zero and , then the value of xyz is-

यदि और हैं , xyz का मान ज्ञात कीजिये –

(A) -1

(B) 0

(C) 1

(D) √2

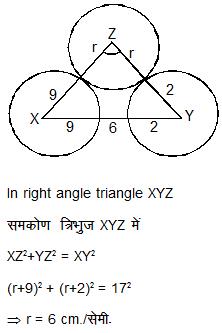
(5) X and Y are centres of circles of radius 9 cm. and 2 cm respectively XY=17 cm. Z is the centre of a circle of radius r cm which touches the above circles externally. Given that - ∠xzy = 90^othe value of r is -

X और Y वृत्त के केन्द्रक हैं, जनकी त्रिज्या क्रमशः 9 सेमी. और 2 सेमी. है। XY=17 सेमी., यदि Z, r वृत्त वाले का केन्द्र है जो दो वृत्त का बाह्य स्पर्श करता है और दिया जाता है ∠xzy = 90^o तो r का मान ज्ञात कीजिए?

(A) 9 cm/सेमी.

(B) 8 cm/सेमी.

(C) 13 cm/सेमी.

(D) 6 cm/सेमी.

(6) ABCD is cyclic quadilateral and O is the centre of the circle . If ∠COD = 140^o and ∠BAC= 40^o, then the value of ∠ BCD is equal to-

ABCD एक चक्रीय चतुर्भुज हैं और वृत्त का केंद्र है | यदि ∠COD = 140^o और ∠BAC= 40^o हैं तो ∠ BCD का मान ज्ञात कीजिये |

(A) 90o

(B) 75o

(C) 70o

(D) 60o

(7) Line 2x + y = 3 and 3x - 2y = 1 meets X-axis at two two points. Find the distance between these points.

रेखा 2x + y = 3 और 3x - 2y = 1 X-अक्ष को 2 बिन्दुओ पर मिलती हैं | इन बिन्दुओ के बीच की दूरी ज्ञात कीजिये ।

(A) 1 units / इकाई

(B) 2 units / इकाई

(C) √5/3 units / इकाई

(D) 2 / 3 units / इकाई

(8) A sum amounts to ₹ 6480 in 4 years and ₹ 9600 in 8 years when it is compounded annually . Find the sum?

एक धनराशि 4 वर्षो में ₹ 6480 और 8 वर्ष में ₹ 9600 हो जाती हैं जब धनराशि चक्रवृद्धि ब्याज पर दी गयी हो | धनराशि ज्ञात कीजिये?

(A) 4300

(B) 4374

(C) 4878

(D) 5438

(9) A person lent Rs. 8000 partly at the rate of 5% and partly at the rate of 6% per annum simple interest. The total interest after 2 years is Rs. 820 then in which ratio will Rs. 8000 is to be divided?

एक व्यक्ति 8000 रूपए का कुछ भाग 5% वार्षिक और शेष भाग 6% वार्षिक साधारण ब्याज की दर पर उधार देता है। दो वर्ष बाद कुल ब्याज 820 रूपए प्राप्त होता है तो 8000 रूपए को किस अनुपात में बांटना होगा?

(A) 13 : 5

(B) 12 : 5

(C) 15 : 4

(D) 7 : 1

(10) Find the maximum number of students among them 1001 pens and 910 pencils can be distributed in such a way that each student gets the same number of pens and same number of pencils.

विद्यार्थियों की अधिकतम संख्या ज्ञात कीजिए जिनमें 1001 पेन और 910 पेंसिले इस प्रकार बांटी जाए कि प्रत्येक को मिले पेनों की संख्या और पेसिंलो की संख्या बराबर हो।

(A) 91

(B) 1001

(C) 910

(D) 1911

Answer Key-

1-Sol-(C)

AG : GD = 2 : 1

AG = BC

AG = BC

GD = BD = DC

AD is a median./AD एक माध्यिका है ।

∠BGC = 90o

According to theorem/प्रमेय के अनुसार,

2-Sol-(A)

Required profit %

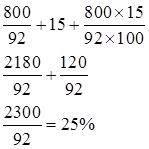
3-Sol-(A)

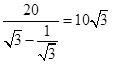
4-Sol-(A)

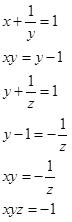
5-Sol-(D)

6-Sol-(C)

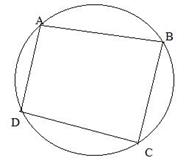
∠CAD = ∠COD/2=70o

∠BAD=70^o+40o

∠BCD= 180^o-110^o=70o

7-Sol-(A)

y₁ = 0,  x₁= 2/3

y₂ = 0, x₂ = 1/3

d = (2/3) + (1/3) = 1 units / इकाई

8-Sol-(B)

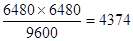
9-Sol-(D)

10-Sol-(A)

910 = 2 × 5 × 7 × 13

1001 = 7 × 11 × 13

HCF/म.स.प. = 91