Dear Readers,
As SSC MTS | CHSL notification is out and candidates have started their preparation for this exam. Mahendras also has started special quizzes for this examination. This series of quizzes are based on the latest pattern of the SSC MTS | CHSL examination. Regular practice of the questions included in the quizzes will boost up your preparations and it will be very helpful in scoring good marks in the examination.
Q-1 What is the simplified value of: 
A. 4x/y
B. x/y
C. 2x/y
D. x/2y
निम्न का सरलीकृत मान क्या है:A. 4x/y
B. x/y
C. 2x/y
D. x/2y
Q-2 A bag contains 6 red balls and 4 blue balls. One red ball weighs 0.35 kg and one blue ball weighs 0.25 kg. How many blue balls are added to the bag, if the average weight decreased by 0.02 kg?
A. 2
B. 3
C. 4
D. 5
एक बैग में 6 लाल गेंद और 4 नीली गेंद हैं| एक लाल गेंद का भार 0.35 किग्रा और 1 नीली गेंद का भार 0.25 किग्रा है| यदि औसत भार में 0.02 किग्रा की कमी हुई है तब बस्ते में कितनी नीली गेंद मिलायी गयी हैं?
A. 2
B. 3
C. 4
D. 5
Q-3 Find the value of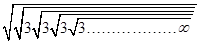 
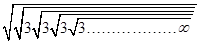
A. 1
B. 2
C. 3
D. Infinite
का मान ज्ञात करेंA. 1
B. 2
C. 3
D. अनंत
Q-4 A 248 m long train running at a speed of 108 km/h overtook another train of length 112 m in 36 seconds. What is the speed of the other train?
A. 66km/hr
B. 70km/hr
C. 72km/hr
D. 75km/hr
108 किमी/घंटा की गति से चलने वाली 248 मीटर लंबी ट्रेन 112 मीटर लंबाई की दूसरी ट्रेन को 36 सेकंड में पार करती है। अन्य ट्रेन की गति कितनी है?
A. 66 कि.मी / घंटा
B. 70 कि.मी / घंटा
C. 72 कि.मी / घंटा
D. 75 कि.मी / घंटा
Q-5 By selling 9 articles for a rupee, a man incurred a loss of 4%. To make a gain of 8%, the number of articles to be sold for a rupee is?
A. 5
B. 6
C. 7
D. 8
9 वस्तुओं को एक रूपये में बेचने पर एक व्यक्ति को 4% की हानि होती है। तो 8% का लाभ अर्जित करने के लिए, एक रूपये में कितनी वस्तुओं को बेचा जाना चाहिए?
A. 5
B. 6
C. 7
D. 8
Q-6 Find the value of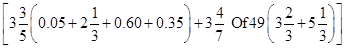 
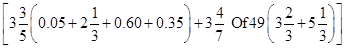
A. 1157
B. 1237
C. 1357
D. 1587
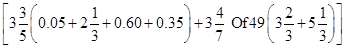का मान ज्ञात कीजियेA. 1157
B. 1237
C. 1357
D. 1587
Q-7 Find the LCM of 0.63, 10.5, 2.1, 4.20.
A. 63
B. 0.63
C. 6.30
D. 6300
0.63, 10.5, 2.1, 4.20 का लघुत्तम समापवर्त्य ज्ञात कीजिए।
A. 63
B. 0.63
C. 6.30
D. 6300
Q-8 How much area to be painted of the rectangular tank measuring 14 m × 12 m × 10 m, if a circular area of radius 1 m is to be left at each surface of the tank?
A. 871.26 m2
B. 883.46 m2
C. 893.16 m2
D. 837.16 m2
14 मीटर × 12 मीटर × 10 मीटर मापने वाले आयताकार टैंक का कितना क्षेत्र चित्रित किया जाना है, अगर टैंक के प्रत्येक सतह पर त्रिज्या 1 मीटर का एक गोलाकार क्षेत्र छोड़ा जाना है?
A. 871.26 मी2
B. 883.46 मी2
C. 893.16 मी2
D. 837.16 मी2
Q-9 If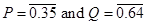 
then find the value of (P + Q)3?
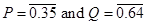then find the value of (P + Q)3?A. 0
B. 1
C. 4
D. 5
यदि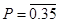 
और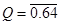
है, तो (P + Q)3 का मान ज्ञात कीजिए
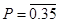और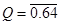है, तो (P + Q)3 का मान ज्ञात कीजिएA. 0
B. 1
C. 4
D. 5
Q-10 What is the value of 2 sin15° cos15° - 4 sin315° cos15°?
A. 3/√2
B. √3/5
C. √3/4
D. ½
2 sin15° cos15° - 4 sin315° cos15°का मान क्या है?
A. 3/√2
B. √3/5
C. √3/4
D. ½
ANSWER KEY -----------
Q-1(4)
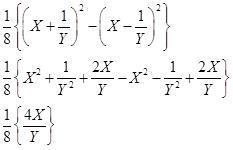
x/2y
Q-2(4)
Weight of 10 balls (6 red + 4 blue) = 6 × 0.35 + 4 × 0.25 = 2.1 + 1 = 3.1 kg
Initial average weight = 3.1/10 = 0.31 kg
Given, decrease in average weight = 0.02 kg
Hence, New average weight = 0.31 – 0.02 = 0.29 kg
Let the number of blue balls added to the bag be ‘x’
Total weight of (10 + x) balls = weight of 6 red balls + weight of (4 + x) blue balls
⇒ (10 + x) × 0.29 = 6 × 0.35 + (4 + x) × 0.25
⇒ 2.9 + 0.29x = 2.1 + 1 + 0.25x
⇒ 0.29x – 0.25x = 3.1 – 2.9
⇒ 0.04x = 0.2
⇒ x = 0.2/0.04
⇒ x = 5
∴ 5 blue balls are added to the bag.
10 गेंदों (6 लाल + 4 नीली) का भार = 6 × 0.35 + 4 × 0.25 = 2.1 + 1 = 3.1 किग्रा
प्रारम्भिक औसत भार = 3.1/10 = 0.31 किग्रा
दिया हुआ है, औसत भार में कमी = 0.02 किग्रा
अतः, नया औसत भार = 0.31 – 0.02 = 0.29 किग्रा
माना बस्ते में मिलायी गयी नीली गेंदों की संख्या x है
(10 + x) गेंदों का कुल भार = 6 लाल गेंदों का भार + (4 + x) नीली गेंदों का भार
⇒ (10 + x) × 0.29 = 6 × 0.35 + (4 + x) × 0.25
⇒ 2.9 + 0.29x = 2.1 + 1 + 0.25x
⇒ 0.29x – 0.25x = 3.1 – 2.9
⇒ 0.04x = 0.2
⇒ x = 0.2/0.04
⇒ x = 5
∴ बस्ते में 5 नीली गेंद मिलायी गयी हैं
Q-3(3)
As we know the property
So
जैसा कि हम को जानते हैं
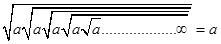
इसलिए
Q-4(3)
As we know,
Speed = Distance/ Time
Total distance = 248 + 112 = 360 m & Time = 36 sec
Speed of first train = 108 km/h = 108 × 5/18 = 30 m/s
Let the speed of the other train be x m/s
Both trains running in the same direction, then relative speed of both trains = (30 – x) m/s
According to the question
30 – x = 360/36
∴ x = 20 m/s = 20 × (18/5) = 72 km/hr
जैसा कि हम जानते हैं,
गति = दूरी/ समय
कुल दूरी = 248 + 112 = 360 मीटर और समय = 36 सेकंड
पहली ट्रेन की गति = 108 किमी/घंटा = 108 × 5/18 = 30 मीटर/सेकंड
माना कि दूसरी ट्रेन की गति x मीटर/सेकंड है।
दोनों ट्रेनें एक ही दिशा में चल रही हैं, तो दोनों ट्रेनों की सापेक्ष गति = (30 – x) मीटर/सेकंड
प्रश्नानुसार,
30 – x = 360/36
∴ x = 20 मीटर/सेकंड = 20 × (18/5) = 72 किमी/घंटा
Q-5(4)
Let cost price (CP) of 9 articles be Rs. x.
Selling price of 9 articles = Re. 1
⇒ x – (4% of x) = 1 (∵ SP = CP – Loss)
⇒ 0.96x = 1
⇒ x = 1/0.96 = Rs. (25/24)
⇒ CP of each article = 25/(24 × 9) = Rs. (25/216)
If Gain = 8%
SP of each article = 1.08 × (25/216) = 1/8
The number of articles to be sold for a rupee = 1/(1/8) = 8
∴ The number of articles to be sold for a rupee = 8
माना कि 9 वस्तुओं का क्रय मूल्य (CP) x रूपये है
9 वस्तुओं का विक्रय मूल्य = 1 रूपये
⇒ x – (x का 4%) = 1 (∵ विक्रय मूल्य = क्रय मूल्य – हानि)
⇒ 0.96x = 1
⇒ x = 1/0.96 = (25/24) रूपये
⇒ प्रत्येक वस्तु का क्रय मूल्य = 25/(24 × 9) = (25/216) रूपये
यदि लाभ = 8%
एक वस्तु का विक्रय मूल्य = 1.08 × (25/216) = 1/8
एक रूपये में बेचीं गई वस्तुओं की संख्या = 1/(1/8) = 8
∴ एक रूपये में बेचीं गई वस्तुओं की संख्या = 8
Q-6(4)
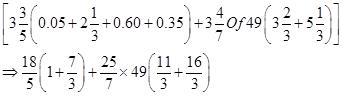
⇒ {18/5 × 10/3 + 175 (27/3)}
⇒ 12 + 1575 = 1587
Q-7(1)
Given numbers are 0.63, 10.5, 2.1, 4.20
Multiply each number with 100, so that decimals parts will be removed.
∴ The numbers are 63, 1050, 210, 420
LCM of 63, 1050, 210, 420 = 2 × 2 × 3 × 3 × 5 × 5 × 7 × 1 = 6300
Again divide the numbers and LCM with 100, we get
⇒ LCM of 0.63, 10.5, 2.1, 4.20 is 63.
दिए गए नंबर 0.63, 10.5, 2.1, 4.20 हैं
प्रत्येक संख्या को 100 के साथ गुणा करें, ताकि दशमलव भागों को हटा दिया जाए |
संख्या 63, 1050, 210, 420 हैं
लघुत्तम समापवर्त्य 63, 1050, 210, 420 = 2 × 2 × 3 × 3 × 5 × 5 × 7 × 1 = 6300
फिर से संख्याओं और लघुत्तम समापवर्त्य को विभाजित करें 100 के साथ, लघुत्तम समापवर्त्य 0.63, 10.5, 2.1, 4.20 का 63 है।
Q-8(4)
As we know,
Length of rectangular tank l = 14 m
Breadth of rectangular tank b = 12 m
Height of rectangular tank h = 10 m
Total surface area of rectangular tank = 2 (lb + bh + hl)
Area of circle = π r2
Total surface area of tank = 2 (14 × 12 + 12 × 10 + 10 × 14) = 2 × 428 = 856 m2
Circular area to be left = π r2 = 3.14 × 1 × 1 = 3.14 m2
As we know, there are six face in rectangular tank, so
total circular area of all six surface to be left = 6 × 3.14 = 18.84 m2
Total area of rectangular tank to be painted = 856 – 18.84 = 837.16 m2
जैसा कि हम जानते हैं,
आयताकार टैंक की लंबाई l = 14 मीटर
आयताकार टैंक की चौड़ाई b = 12 मीटर
आयताकार टैंक की ऊंचाई h = 10 मीटर
आयताकार टैंक की कुल सतह क्षेत्र = 2 (lb + bh + hl)
वृत्त का क्षेत्रफल = 2r2
टैंक की कुल सतह क्षेत्र = 2 (14 × 12 + 12 × 10 + 10 × 14) = 2 × 428 = 856 मी2
परिपत्र क्षेत्र को छोड़ा जाना = 2 r2 = 3.14 × 1 × 1 = 3.14 मी2
जैसा कि हम जानते हैं, आयताकार टैंक में छह सतह होते हैं, इसलिए
छोड़े जाने के लिए सभी छह सतह का कुल गोलाकार क्षेत्र = 6 × 3.14 = 18.84 मी2
आयताकार टैंक का कुल क्षेत्र चित्रित किया जाना है = 856 - 18.84 = 837.16 मी2
Q-9(2)
⇒ P = 0.353535 ----(1)
Multiply by 100 in equation (1)
⇒ 100P = 35 + 0.3535….
⇒ 100P = 35 + P
⇒ 99P = 35
⇒ P = 35/99
Similarly,
⇒ Q = 64/99
⇒ (P + Q) = (35/99) + (64/99) = 99/99
⇒ (P + Q)3 = 13 = 1
⇒ P = 0.353535 ----(1)
समीकरण(1) में 100 से गुणा करें
⇒ 100P = 35 + 0.3535….
⇒ 100P = 35 + P
⇒ 99P = 35
⇒ P = 35/99
उसी प्रकार
⇒ Q = 64/99
⇒ (P + Q) = (35/99) + (64/99) = 99/99
⇒ (P + Q)3 = 13 = 1
Q-10(3)
cos A = √[(1 + cos 2A) /2]
∴ cos 15° = √[(1 + cos 30°) /2]
⇒ √[(2 + √3) /4]
⇒ √[(4 + 2√3)/8] = (√3 + 1) / (2√2)
2 sin 15° cos 15° - 4 sin315° cos15° = 3sin 15° cos 15° - 4 sin315° cos15° - sin 15° cos 15°
⇒ cos 15° × (3 sin15° - 4sin315°) - (2 sin15° cos15°) /2
⇒ cos 15° × sin 45° - sin 30°/2 [∵ 3 sinA - 4sin3A = sin3A, 2 sinA cosA = sin2A]
⇒ (√3 + 1) / (2√2) × 1/√2 - ¼
⇒ √3/4
0 comments:
Post a Comment
MAHENDRA GURU