Dear Readers,
As SSC MTS | CHSL notification is out and candidates have started their preparation for this exam. Mahendras also has started special quizzes for this examination. This series of quizzes are based on the latest pattern of the SSC MTS | CHSL examination. Regular practice of the questions included in the quizzes will boost up your preparations and it will be very helpful in scoring good marks in the examination.
Q-1 The area of a rectangle whose length is 5 units more than twice its width is 75 square units. What is its width?
A. 3
B. 5
C. 7
D. 10
एक आयत का क्षेत्रफल जिसकी लंबाई उसकी चौड़ाई के दोगुने से 5 इकाई अधिक है, 75 वर्ग इकाई है। इसकी चौड़ाई क्या है?
A. 3
B. 5
C. 7
D. 10
Q-2 The value of 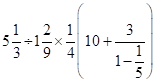 is
is
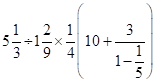 is
isA. 15
B. 67/25
C. 128/11
D. 128/99
 का मान है
का मान हैA. 15
B. 67/25
C. 128/11
D. 128/99
Q-3 Find the value of 2 (sin6 θ
+ cos6 θ) – 3 (sin4 θ+ cos4 θ) .
A. 1
B. 0
C. – 1
D. 2
2 (sin6 θ
+ cos6 θ) – 3 (sin4 θ+ cos4 θ) का मान ज्ञात कीजिये ।
A. 1
B. 0
C. – 1
D. 2
Q-4 From a solid cylinder of height 4 cm. and radius 3 cm, a conical cavity of height 4 cm. and of base radius 3 cm. is hollowed out. What is the total surface area of the remaining solid?
A. 15π cm.2
B. 22π cm.2
C. 33π cm.2
D. 48π cm.2
4 सेमी. ऊँचाई और 3 सेमी. त्रिज्या के एक ठोस बेलन से 4 सेमी. ऊँचाई और आधार त्रिज्या 3 सेमी. की एक शांकव गुहिका खोद निकाली जाती है। बचे हुए ठोस का कुल पृष्ठ क्षेत्रफल क्या है?
A. 15π सेमी.2
B. 22π सेमी.2
C. 33π सेमी.2
D. 48π सेमी.2
Q-5 The fourth proportional to 7, 11, 14 is
A. 16
B. 18
C. 20
D. 22
7, 11, 14 का चौथा समानुपातिक क्या है?
A. 16
B. 18
C. 20
D. 22
Q-6 A, B and C can do a piece of work in 20, 30 and 60 days respectively. How many days does it needed to complete the work if A does the work and he is assisted by B and C on every third day?
A. 10
B. 14
C. 15
D. 9
A, B और C क्रमशः 20, 30 और 60 दिनों में एक काम को कर सकते हैं। काम को पूरा करने के लिए कितने दिन की आवश्यकता है यदि A कार्य करता है और उसे हर तीसरे दिन B और C द्वारा सहायता दी जाती है?
A. 10
B. 14
C. 15
D. 9
Q-7 If sec θ = 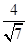 , then the value of
, then the value of 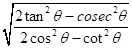 is
is
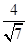 , then the value of
, then the value of 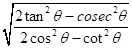 is
isA. 20/7
B. 0
C. 4
D. None of these
यदि sec θ = 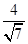 , तो
, तो 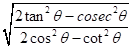 का मान है
का मान है
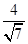 , तो
, तो 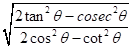 का मान है
का मान हैA. 20/7
B. 0
C. 4
D. इनमें से कोई नहीं
Q-8 Find the length of the tangent drawn from a point whose distance from the centre of a circle is 25 cm. Given that the radius of the circle is 7cm.
A. 12 cm.
B. 18 cm.
C. 24 cm.
D. 28 cm.
उस स्पर्श रेखा की लम्बाई ज्ञात कीजिए जोकि वृत्त के केंद्र से 25 सेमी दूरी पर स्थित किसी बिन्दु से खींची जाती है। दिया है कि वृत्त की त्रिज्या 7 सेमी है।
A. 12 सेमी.
B. 18 सेमी.
C. 24 सेमी.
D. 28 सेमी.
Q-9 For a triangle PQR, S and T are two points on PQ and PR such that PS = 1/4 PQ, PT = 1/4 PR. If QR = 12 cm, then ST is
A. 4 cm.
B. 3 cm.
C. 6 cm.
D. 5 cm.
एक त्रिभुज PQR के लिए, S और T दो बिन्दु PQ और PR पर ऐसे हैं कि PS = 1/4 PQ, PT = 1/4 PR. यदि QR = 12 सेमी, तो ST है
A. 4 सेमी.
B. 3 सेमी.
C. 6 सेमी.
D. 5 सेमी.
Q-10 A shopkeeper allows two successive discounts on an article whose marked price is Rs. 150 and selling price is Rs. 105. What is first discount if second discount is 12.5%?
A. 25%
B. 17.5%
C. 20%
D. 16.67%
एक दुकानदार किसी वस्तु पर दो क्रमिक छूट देता है। जिसका अंकित मूल्य 150 रूपये है। और विक्रय मूल्य 105 रूपये हैं यदि दूसरी छूट 12.5% हो तो पहली छूट क्या है?
A. 25%
B. 17.5%
C. 20%
D. 16.67%
ANSWER:-
Q-1(2)
l = (2b + 5)
l × b = 75
(2b + 5) × b = 75
2b2 + 5b – 75 = 0
2b2 + 15b – 10b – 75 = 0
(2b + 15) (b – 5) = 0
b = 5
Q-2(1)
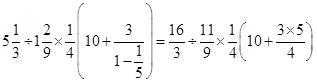
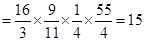
Q-3(3)
Q-4(4)
Total surface area of the remaining solid = 2r π h + π r2 + π rl
= 2 × 3 × 4 × π + 9 π + π × 3 × 5
= 24 π + 9 π + 15 π
= 48 π
cm.2
शेष ठोस का कुल पृष्ठ क्षेत्रफल =2r π h + π r2 + π rl
= 2 × 3 × 4 × π + 9 π + π × 3 × 5
= 24 π + 9 π + 15 π
= 48 π
सेमी.2
Q-5(4)
Let fourth proportional be x.
7: 11 :: 14: x
7 × x = 11 × 14
x = 22
माना चौथा समानुपातिक x है ।
7: 11 :: 14: x
7 × x = 11 × 14
x = 22
Q-6(3)
3 A 20
2 B 30
1 C 60
Total work in 3 days = (3 × 3 + 2 + 1) = 12 units
Number of such cycles = 60 ÷ 12 = 5
Number of days = 5 × 3 = 15 days
3 A 20
2 B 30
1 C 60
3 दिन में किया गया कुल काम = (3 × 3 + 2 + 1) = 12 मात्रक
ऐसे चक्रों की संख्या = 60 ÷ 12 = 5
दिनों की संख्या = 5 × 3 = 15 दिन
Q-7(1)
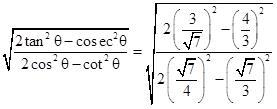
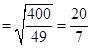
Q-8(3)
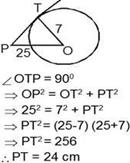
Q-9(2)
By similarity,
ST = 1/4QR
ST = 1/4× 12 = 3 cm.
समरूपता से:
ST = 1/4QR
ST = 1/4× 12 = 3 सेमी.
Q-10(3)
Let first discount be x%.
105 = 150 ×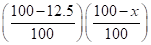
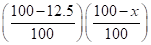
10500 = 15 × 875 × (100 – x)
80 = 100 – x
x = 100 – 80 = 20%
माना पहली छूट x% है ।
105 = 150 ×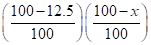
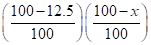
10500 = 15 × 875 × (100 – x)
80 = 100 – x
x = 100 – 80 = 20%







0 comments:
Post a Comment
MAHENDRA GURU